群体遗传模拟

这里记录群体模拟的原理和方法。

群体模拟

参考数据

我们需要两个参考数据集：map.rds 和 LD_chr1.rds 。

这里使用欧洲人群的参考LD数据和基因频率数据 （ European LD reference ）进行模拟。具体来说，这是一个关于欧洲人群的连锁不平衡 (LD, Linkage Disequilibrium) 参考数据集。

该数据集 LD_chr1.rds 包含欧洲人群的基因组数据（这里只考虑1号染色体），包括：

• 基因型数据（SNP信息）
• LD矩阵，描述了不同SNP之间的关联程度

通常用于基因组学研究，如基因-环境互动分析、全基因组关联研究（GWAS）等。

此外我们还需要一个映射表 map.rds ，包含这些SNP的等位基因及其频率信息：

map.rds 各列的解释：

• chr：染色体编号。
• pos：染色体上的位置。
• a0：SNP的一个等位基因（A、G、C、T）。
• a1：另一个等位基因。
• rsid：参考SNP标识符（例如rs3131972）。
• af_UKBB：在UK Biobank人群中的等位基因频率。
• ld：连锁不平衡（LD）值，量化了两个遗传变异之间的相关性。
• pos_hg17、pos_hg18、pos_hg38：SNP在不同版本的人类基因组参考中的位置（hg17、hg18、hg38）。

模拟详解

示例

为了帮助更好地理解基因型模拟和表型模拟的数学过程，这里构建一个低维的示例。我将使用一个简化的案例，其中包含几个基本的步骤，模拟少量的样本和SNP（3个SNP和2个样本）。

步骤 1: 初始化等位基因频率 $P$

假设有3个SNP，且它们的等位基因频率如下：

$$P = [0.3, 0.5, 0.7]$$

步骤 2: 协方差矩阵 $COV$ 的计算

假设我们有2个样本，且3个SNP之间的连锁不平衡（LD）矩阵如下（这是一个简化的例子）：

$$\text{LD} = \begin{bmatrix} 1.0 & 0.5 & 0.2 \\ 0.5 & 1.0 & 0.3 \\ 0.2 & 0.3 & 1.0 \end{bmatrix}$$

接下来，我们计算协方差矩阵 $COV$。

协方差矩阵 $COV$ 可以通过连锁不平衡矩阵 $LD$ 和等位基因频率矩阵 $P$ 来计算。具体来说，对于给定的连锁不平衡矩阵 $LD$，等位基因频率矩阵 $P$，我们可以使用以下公式来计算协方差矩阵 $COV$：

$$COV_{ij} = \text{LD}_{ij} \cdot \sqrt{P_i \cdot (1 - P_i) \cdot P_j \cdot (1 - P_j)}$$

其中：

• $COV_{ij}$ 是 $SNP_i$ 和 $SNP_j$ 之间的协方差；
• $\text{LD}_{ij}$ 是 $SNP_i$ 和 $SNP_j$ 之间的连锁不平衡（LD）系数；
• $P_i$ 和 $P_j$ 分别是 $SNP_i$ 和 $SNP_j$ 的等位基因频率；
• $P_i (1 - P_i)$ 表示 $SNP_i$ 的基因型的方差（即该SNP的变异性）。

$COV_{11}$：SNP1与自身的协方差

$$COV_{11} = \text{LD}_{11} \cdot \sqrt{P_1 \cdot (1 - P_1) \cdot P_1 \cdot (1 - P_1)} = 1.0 \cdot \sqrt{0.3 \cdot 0.7 \cdot 0.3 \cdot 0.7} = 0.1$$

$COV_{12}$：SNP1与SNP2的协方差

$$COV_{12} = \text{LD}_{12} \cdot \sqrt{P_1 \cdot (1 - P_1) \cdot P_2 \cdot (1 - P_2)} = 0.5 \cdot \sqrt{0.3 \cdot 0.7 \cdot 0.5 \cdot 0.5} = 0.05$$

$COV_{13}$：SNP1与SNP3的协方差

$$COV_{13} = \text{LD}_{13} \cdot \sqrt{P_1 \cdot (1 - P_1) \cdot P_3 \cdot (1 - P_3)} = 0.2 \cdot \sqrt{0.3 \cdot 0.7 \cdot 0.7 \cdot 0.3} = 0.02$$

其余的类似计算。通过计算，协方差矩阵 $COV$ 给出：

$$COV = \begin{bmatrix} 0.1 & 0.05 & 0.02 \\ 0.05 & 0.1 & 0.03 \\ 0.02 & 0.03 & 0.1 \end{bmatrix}$$

步骤 3: 生成正态分布随机数 $z_i$

我们已经知道了每个SNP的等位基因频率和它们之间的连锁不平衡（LD）。我们想要生成一个具有这些特征的基因型数据。

为了做到这一点，我们需要从一个正态分布随机数（$z_i$）开始，且这些随机数需要被转化为符合我们期望的协方差结构的基因型数据。因为协方差矩阵 $COV$ 描述了不同SNP之间的相关性，而我们希望生成的数据能够遵循这种相关性。

对于每个样本，我们生成一个标准正态分布的随机数向量。假设我们有2个样本，生成的正态分布随机数如下：

$$z_1 = [z_{11}, z_{12}, z_{13}] = [0.7, -1.2, 0.5]$$

$$z_2 = [z_{21}, z_{22}, z_{23}] = [-0.4, 0.8, -0.3]$$

步骤 4: 使用下三角矩阵 $L$（ Cholesky 分解） 进行变换

我们用下三角矩阵 $L$ 对正态分布随机数进行线性变换，是为了确保生成的基因型数据 $y_i$ 满足以下两个条件：

1. 基因型数据之间的相关性（协方差）：$L$ 是协方差矩阵 $COV$ 的 Cholesky 分解结果，因此通过对随机数 $z_i$ 进行线性变换，能够确保生成的基因型数据之间的协方差结构符合我们设定的目标协方差矩阵 $COV$。也就是说，$L$ 通过调整样本之间的关系，确保SNP之间的相关性被正确模拟。
2. 标准化：因为基因型数据应该满足特定的方差（通常是 $0$、$1$ 或 $2$），而每个SNP的基因型是离散的（即0、1、2表示不同的基因型类型），我们希望将生成的基因型数据进行标准化处理，使它们符合目标分布的形状。通过线性变换，$L$ 可以帮助调整基因型的分布，使得每个样本的基因型数据具有期望的统计特性。

协方差矩阵 $COV$ 需要进行Cholesky分解来得到下三角矩阵 $L$。

Cholesky分解是将一个对称正定矩阵分解为一个下三角矩阵 $L$ 和它的转置矩阵 $L^T$ 的乘积。换句话说，对于一个对称正定矩阵 $COV$，我们可以通过如下的分解方式得到：

$$COV = L \cdot L^T$$

其中，$L$ 是下三角矩阵，假设协方差矩阵 $COV$ 为：

$$COV = \begin{bmatrix} 0.1 & 0.05 & 0.02 \\ 0.05 & 0.1 & 0.03 \\ 0.02 & 0.03 & 0.1 \end{bmatrix}$$

我们需要找到下三角矩阵 $L$：

$$L = \begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{bmatrix}$$

根据Cholesky分解的定义，$COV = L \cdot L^T$，即：

$$\begin{bmatrix} 0.1 & 0.05 & 0.02 \\ 0.05 & 0.1 & 0.03 \\ 0.02 & 0.03 & 0.1 \end{bmatrix} = \begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{bmatrix} \begin{bmatrix} l_{11} & l_{21} & l_{31} \\ 0 & l_{22} & l_{32} \\ 0 & 0 & l_{33} \end{bmatrix}$$

通过矩阵乘法，我们得到：

$$\begin{bmatrix} 0.1 & 0.05 & 0.02 \\ 0.05 & 0.1 & 0.03 \\ 0.02 & 0.03 & 0.1 \end{bmatrix} = \begin{bmatrix} l_{11}^2 & l_{11}l_{21} & l_{11}l_{31} \\ l_{11}l_{21} & l_{21}^2 + l_{22}^2 & l_{21}l_{31} + l_{22}l_{32} \\ l_{11}l_{31} & l_{21}l_{31} + l_{22}l_{32} & l_{31}^2 + l_{32}^2 + l_{33}^2 \end{bmatrix}$$

我们通过对比矩阵的相应元素来求解下三角矩阵的元素。

首先，根据 $COV$ 矩阵的第 (1, 1) 元素，我们得到：

$$l_{11}^2 = 0.1 \quad \Rightarrow \quad l_{11} = \sqrt{0.1} = 0.316$$

根据 $COV$ 矩阵的第 (2, 1) 元素，我们得到：

$$l_{11} \cdot l_{21} = 0.05 \quad \Rightarrow \quad l_{21} = \frac{0.05}{l_{11}} = \frac{0.05}{0.316} = 0.158$$

根据 $COV$ 矩阵的第 (2, 2) 元素，我们得到：

$$l_{21}^2 + l_{22}^2 = 0.1$$

$$\Rightarrow \quad l_{22} = \sqrt{0.075} = 0.273$$

其余元素的计算类似。最终得到的下三角矩阵 $L$ 是：

$$L = \begin{bmatrix} 0.316 & 0 & 0 \\ 0.158 & 0.273 & 0 \\ 0.063 & 0.109 & 0.285 \end{bmatrix}$$

这个矩阵就是协方差矩阵 $COV$ 的 Cholesky 分解结果。

现在，我们用这个下三角矩阵 $L$ 对样本的正态分布随机数 $z_i$ 进行线性变换，得到标准化后的基因型数据 $y_i$。

对于样本1：

$$y_1 = L \cdot z_1 = \begin{bmatrix} 0.316 & 0 & 0 \\ 0.158 & 0.273 & 0 \\ 0.063 & 0.109 & 0.285 \end{bmatrix} \cdot \begin{bmatrix} 0.7 \\ -1.2 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.221 \\ -0.063 \\ 0.169 \end{bmatrix}$$

对于样本2：

$$y_2 = L \cdot z_2 = \begin{bmatrix} 0.316 & 0 & 0 \\ 0.158 & 0.273 & 0 \\ 0.063 & 0.109 & 0.285 \end{bmatrix} \cdot \begin{bmatrix} -0.4 \\ 0.8 \\ -0.3 \end{bmatrix} = \begin{bmatrix} -0.126 \\ 0.295 \\ -0.163 \end{bmatrix}$$

步骤 5: 从标准化的基因型数据中生成基因型值

在每个样本的标准化基因型数据生成后，根据每个SNP的等位基因频率（P）对基因型进行离散化。离散化的目标是将连续的基因型数据映射到 0、1或2（分别表示基因型AA、AB和BB）。

离散化过程的具体步骤：

1. 计算等位基因频率的阈值：
   • p：某个SNP的A等位基因频率。
   • q=1-p：B等位基因的频率。
   • p² 和 2pq 的阈值位置：p² 是AA基因型的频率，2pq 是AB基因型的频率。
2. 排序标准化基因型：将标准化后的基因型数据进行排序。
3. 根据阈值离散化标准化基因型：
   • 将每个样本的标准化基因型与排序后的标准化基因型比较，基于阈值位置判断其属于哪种基因型。
     • 如果标准化基因型小于等于p²阈值的位置，分配为基因型AA（0）。
     • 如果标准化基因型在p²和p² + 2pq之间，分配为基因型AB（1）。
     • 如果标准化基因型大于p² + 2pq，分配为基因型BB（2）。

通过这种方法，标准化基因型被映射到AA、AB和BB基因型，同时考虑了不同等位基因频率的影响。

这种离散化方法是基于等位基因频率来将连续数据划分为离散的基因型类别，模拟现实中基因型的分布特征。

步骤 6: 生成表型数据

因果效应（Effect）是指某个特定SNP（单核苷酸多态性）对表型的影响。

因果效应是如何得到的？

因果效应的大小通常与表型的遗传率（heritability）相关。遗传率 $H_g^2$ 是指表型方差中由基因因素解释的部分。在模拟表型时，我们使用这种遗传率来控制因果效应的分布。

因果效应 $\text{Effect}_i$ 一般会从一个正态分布中抽取，分布的方差通常与遗传率、样本量以及SNP的数量有关。公式为：

$$\text{Effect}_i = \mathcal{N}\left( 0, \frac{H_g^2}{n \cdot p} \right)$$

其中：

• $\mathcal{N}(0, \sigma^2)$ 是均值为零，方差为 $\sigma^2$ 的正态分布；
• $n$ 是SNP的数量；
• $p$ 是有非零因果效应的SNP的比例；
• $H_g^2$ 是遗传率，决定了表型中由基因效应解释的方差。

如何从分布中生成因果效应？

假设我们有3个SNP，且表型的遗传率 $H_g^2 = 0.5$，有80%的SNP是有因果效应的。我们可以从一个均值为0、标准差为 $\frac{H_g^2}{n \cdot p}$ 的正态分布中抽取因果效应值。

假设我们的目标是模拟因果效应，并且我们知道：

• $n = 3$（SNP的数量），
• $p = 0.8$（80%的SNP有效应），
• $H_g^2 = 0.5$（遗传率）。

则每个SNP的因果效应可以从如下正态分布中抽取：

$$\text{Effect}_i \sim \mathcal{N}\left( 0, \frac{0.5}{3 \times 0.8} \right) = \mathcal{N}(0, 0.2083)$$

这意味着每个SNP的因果效应会从均值为0、方差为0.2083的正态分布中抽取。模拟结果可能是：

• $\text{Effect}_1 = 0.5$（从分布中抽取的正效应），
• $\text{Effect}_2 = -0.3$（从分布中抽取的负效应），
• $\text{Effect}_3 = 0.1$（从分布中抽取的小正效应）。

假设遗传方差 $H_g^2 = 0.4$，噪声项 $\epsilon_j$ 服从正态分布 $\mathcal{N}(0, 1 - H_g^2)$。

表型值 $y_j$ 是通过将每个SNP的标准化基因型 $Z_{j,i}$ 和该SNP的因果效应 $\text{Effect}_i$ 进行线性组合得到的。再加上一个噪声项 $\epsilon_j$：

$$y_j = \sum_{i=1}^{n} Z_{j,i} \cdot \text{Effect}_i + \epsilon_j$$

其中：

• $\text{Effect}_1 = 0.5$
• $\text{Effect}_2 = -0.3$
• $\text{Effect}_3 = 0.1$

对于样本1，表型值 $y_1$ 的计算如下：

$$y_1 = (1.732 \times 0.5) + (-1.414 \times -0.3) + (-2.309 \times 0.1) + \epsilon_1$$

假设噪声项 $\epsilon_1 = 0.2$，那么：

$$y_1 = 0.866 + 0.424 - 0.231 + 0.2 = 1.259$$

类似地，可以计算样本2的表型值。

通过这个低维示例，演示了如何初始化等位基因频率，计算协方差矩阵，生成基因型数据，并最终模拟表型值。这个过程是基于正态分布、协方差矩阵、基因型效应以及噪声项的线性组合来模拟人群中的表型数据。

在实际应用中，需要更多的SNP、样本以及更复杂的基因型和表型之间的关系。

程序模拟

R代码模拟：

# 加载必需的R包
library(MASS)    # 包含许多统计和线性模型的函数
library(hapsim)  # 用于模拟基因型数据和生成单倍型数据
library(bigsnpr) # 处理大规模基因组数据，尤其是单核苷酸多态性（SNP）数据
library(bigreadr) # 用于处理大型数据集，帮助高效读取和处理数据

#' 基于LD矩阵和等位基因频率模拟基因型数据
#' @param snps_num 需要模拟的SNP数量
#' @param sample_size 样本量
#' @param chr 染色体号（默认：1）
#' @return 包含模拟基因型数据及相关信息的列表
genotypeSim <- function(snps_num, sample_size, chr=1) {
  # 加载参考数据
  map_ldref <- readRDS("map.rds")
  LD_ref <- readRDS("LD_chr1.rds")
  
  # 筛选指定染色体的数据
  map_ldref <- map_ldref[map_ldref$chr == chr,]
  
  # 随机选择一段连续的SNP区域
  start_sim <- max(1, as.integer(runif(1) * (dim(map_ldref)[1] - snps_num)))
  end_sim <- start_sim + snps_num - 1
  
  
  # 提取选定SNP的相关数据
  map_sim <- map_ldref[seq(start_sim, end_sim),]
  cor_sim <- LD_ref[seq(start_sim, end_sim), seq(start_sim, end_sim)]
  
  # 使用hapsim包计算协方差矩阵
  N <- snps_num
  C <- cor_sim
  P <- map_sim$af_UKBB  # 等位基因频率
  Q <- qnorm(P)
  
  # 使用hapsim的C函数计算协方差矩阵
  # .C() 是一个允许R调用C语言函数的接口，它可以将R数据转换为C语言的数据格式，并将计算结果返回给R
  vmat <- .C("covariance", 
             as.integer(N), 
             as.double(C), 
             as.double(P), 
             as.double(Q), 
             rlt = as.double(as.matrix(rep(0, N*N))), 
             PACKAGE = "hapsim")$rlt
  
  V <- matrix(vmat, nrow = N, ncol = N)
  if (!checkpd(V)) V <- makepd(V)  # 确保矩阵正定
  
  # 创建用于模拟的数据列表
  x <- list(freqs = P, cor = C, cov = V)
  
  # 生成单倍型数据并转换为双倍型
  y <- haplosim(sample_size, x)
  y$data <- 2 - y$data - y$data[sample(seq(sample_size), sample_size),]
  
  return(y)
}

#' 模拟GWAS汇总统计量
#' @param snps_num SNP数量
#' @param sample_size 样本量
#' @param filename 输出文件名前缀
#' @param trait 性状类型（"quantity"数量性状或"quality"质量性状）
#' @param Hg2 遗传力
#' @param p 致病变异比例
#' @param prevelence 疾病患病率（用于质量性状）
gwasSummarySim <- function(snps_num, sample_size, filename="default", 
                           trait="quantity", Hg2=0.03, p=0.01, prevelence=0.1) {
  # 生成基因型数据
  y <- genotypeSim(snps_num, sample_size)
  
  # 使用稀疏模型生成因果效应
  causal_effect <- rnorm(snps_num, 0, sqrt(Hg2/(snps_num*p)))
  causal_effect[runif(snps_num, 0, 1) > p] <- 0  # 将非致病变异效应设为0
  
  # 标准化基因型
  X <- t((t(y$data) - 2 * y$freqs)/(sqrt(2 * y$freqs*(1 - y$freqs))))
  
  # 生成表型得分
  phenotype_score <- colSums(apply(y$data, MARGIN=1, 
                                   FUN=function(X){return(X * causal_effect)})) + 
    rnorm(sample_size, 0, sqrt(1-Hg2))
  
  # 将表型值和基因型数据合并
  phenotype_data <- data.frame(phenotype = phenotype_score)
  genotype_data <- as.data.frame(t(y$data))  # 转置基因型数据，以每行表示一个样本
  
  # 合并表型和基因型数据
  combined_data <- cbind(phenotype_data, genotype_data)
  
  # 保存合并后的数据为CSV
  write.csv(combined_data, paste0(filename, "_genotype_phenotype.csv"), row.names = FALSE)
  
  # 初始化结果数据框
  gwas_summary <- data.frame(matrix(0, nrow=snps_num, ncol=4))
  names(gwas_summary) <- c("BETA", "SE", "Zscore", "P")
  
  if(trait == "quantity") {
    # 数量性状分析
    for(i in seq(snps_num)) {
      relation <- lm(phenotype_score ~ y$data[,i])
      gwas_summary[i,] <- summary(relation)$coefficients[2,]
    }
  } else {
    # 质量性状分析
    threshold <- quantile(phenotype_score, 1 - prevelence)
    phenotype <- ifelse(phenotype_score > threshold[1], 1, 0)
    
    for(i in seq(snps_num)) {
      relation <- glm(phenotype ~ y$data[,i], family=binomial())
      gwas_summary[i,] <- summary(relation)$coefficients[2,]
    }
  }
  
  # 保存结果
  write.csv(gwas_summary, paste0(filename, "_gwasSummary.csv"))
  
  # 记录关键信息并保存
  heritability <- Hg2                      # 记录遗传力
  disease_variants <- p                    # 记录致病变异比例
  
  # 创建包含关键信息的数据框
  metadata <- data.frame(
    heritability = heritability,
    disease_variants = disease_variants,
    causal_effect = paste(round(causal_effect, 4), collapse = ",")  # 将因果效应存储为逗号分隔的字符串
  )
  
  # 保存关键信息为CSV
  write.csv(metadata, paste0(filename, "_metadata.csv"), row.names = FALSE)
  
  return(gwas_summary)
}

Java模拟的代码已上传至 github ：

https://github.com/luoying2002/Genotype-Phenotype-Simulation

public static void main(String[] args) throws IOException {

        String basePath = "/Users/yiguoshabi/Desktop/这是真研究/QuantTraitPredictor/resources/simulation/";

        String CCF_MAP = basePath + "map.ccf";
        String LD_chr1 = basePath + "LD_chr1.ccf";

        int CHR = 1;
        int N = 100;
        int snpsNum = 1000;
        double modifyRate = 0.01;
        double Hg2 = 0.6;
        double p = 0.1;

        GenotypeSim genotypeSim = new GenotypeSim(CCF_MAP, LD_chr1, CHR, N, snpsNum, modifyRate);

        PhenotypeSim phenotypeSim  = new PhenotypeSim(genotypeSim, Hg2, p);

        phenotypeSim.exportAll(basePath + "simulation");

        phenotypeSim.gwasSummary2csv(basePath + "simulation_gwas_summary.csv");

    }

运行此程序：

在R中，绘制QQ图检验模拟的好坏：

library(qqman)
gwasSummary <- "simulation_gwas_summary.csv"
# 读取 CSV 文件
gwas_data <- read.csv(gwasSummary, fileEncoding = "UTF-8", stringsAsFactors = FALSE)
# 查看数据
head(gwas_data)
qq(gwas_data$P)

结果：

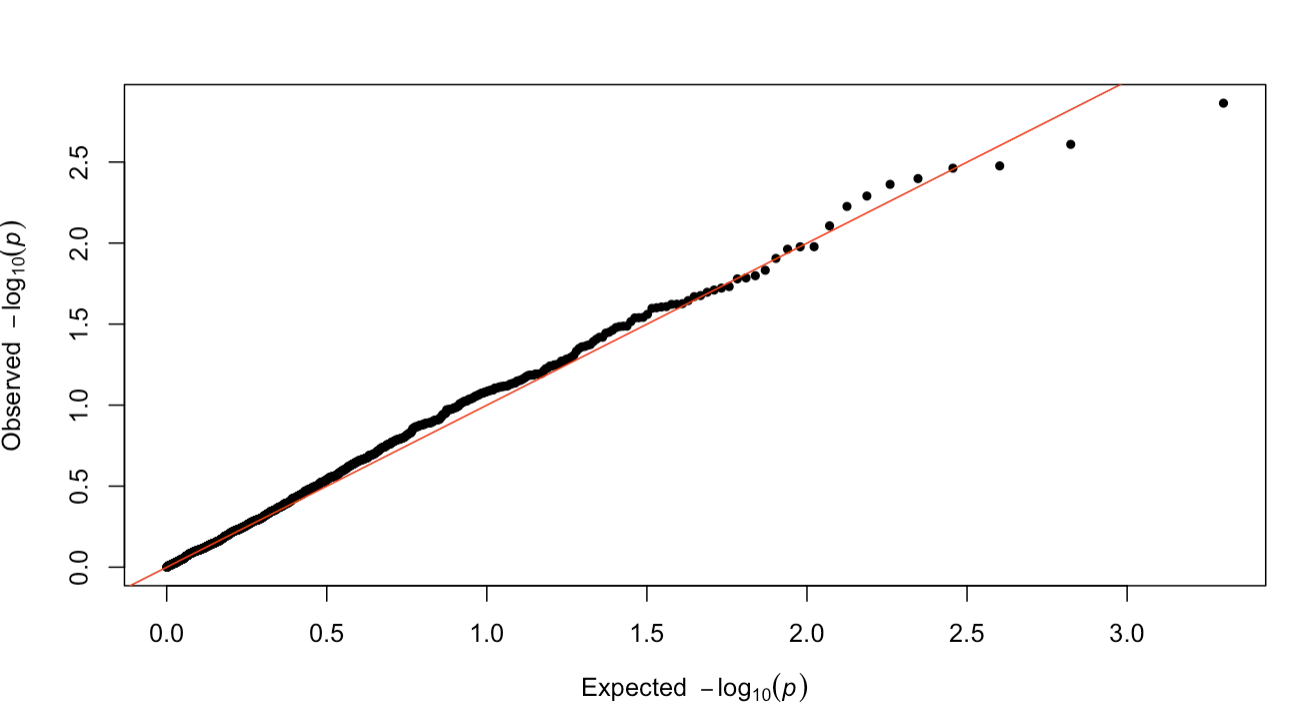
整体效果还是可以的。